[最も人気のある！] 2tanx/1 tan^2x is equal to 131061

Sin(2x) = (2tan(x)) / (1tan^2(x)) *** Start with RHS 2tanx/(1tan^2x) 2tanx/(sec^2x) 2(sinx/cosx)/(1 1 Expert Answer 1sin2x = 12sinxcosx = sin^2x cos^2x 2sinxcosx = (sinx cosx)^2 = an alternate way of expressing 1sin2x > if this is what you were looking for What is Tan2x formula?Prove as an identity;

What Is The Formula Of Tan2x Quora

2tanx/1 tan^2x is equal to

2tanx/1 tan^2x is equal to-Watch Video in App This browser does not support the video element1 What two common identities are most useful for simplifying 2tanx/(sin^2x cos^2x tan^2x)?

If F X Tan 2x Then

 Transcript Ex 76, 24 ∫1 𝑒^𝑥 sec⁡𝑥 (1tan⁡𝑥 )𝑑𝑥 "ex" cos x C (B) "ex" sec x C "ex" sin x C (D) 𝑒𝑥 tan x C ∫1 𝑒^𝑥 sec⁡𝑥 (1tan⁡𝑥 )𝑑𝑥 = ∫1 𝑒^𝑥 (sec⁡𝑥sec⁡𝑥 tan⁡𝑥 )𝑑𝑥 It is of the form ∫1 〖𝑒^𝑥 𝑓(𝑥)𝑓^′ (𝑥) 〗 𝑑𝑥=𝑒^𝑥 𝑓(𝑥)𝐶 Where 𝑓(𝑥)=sec⁡𝑥 𝑓Click here👆to get an answer to your question ️ The value of f(0) so that the function f(x) = log(1 x^2tan x)sin x^3 , x = 0 continuous at x = 0, isOR going clockwise/counterclockwise around three inside triangles starting at the bottom and using subtraction, eg, 1cos^2x=sin^2x Law of Sines sinA/a=sinB/b=sinC/c capital = angle, lowercase = side to find theta, use inv sin;

You can put this solution on YOUR website! Lemma 1 cot 2x = (1/2)cot x tan x Proof (1) cot 2x = 1/tan(2x) = cos(2x)/sin(2x) See here for definition of tan (2) cos(2x) = cos 2 (x) sin 2 (x) See LemmaProve that $\tan^6 °\tan^6 40°\tan^6 80°$ is an integer 1 Find the solution set of the equation $5(\frac{1}{25})^{\sin^2x}45^{\cos2x}=25^{\frac{\sin2x}{2}}$

Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formulaUsing the answer for what Tan(3x) equals, now i need to plug that in to solve for Tan(4x) Tan (4x)=Tan(3xx) so Tan(3xx)= tan3xtanx/1Tan3x(tanx) PLease solve and show all work to show what RHS equalsTwo identities are sin^2x cos^2x = 1 and tan2x=2tanx/1tan^2x calculus find the derivative of the functions F(x)= tan^2(x) and G(x) = sec^2(x) based on your calculations what can you say about F(x) G(x) I found F'x =2 secx^2tanx G'(x)= 2secx^2tanx then when subtracted they equal

Tan2x ただの悪魔の画像

Limit X Tends P 4 Sec 2x 2 Tanx 1 Brainly In

M1docx Solve(2tanx(1 tan 2 x We have to solve(2tanx(1 tan 2 x Solution(2tanx(1 tan^2x = 21\/tan(x)=tan(x = 2(sin(x cos(x(sin(x)cos(x 2 2 = If(2tanx/(1tan^2x))=1, then x can equal? Tyrion101 said But is it equal to (2tanx/1tan^2x)^2 is what I'm asking I may have been unclear Yes and no means , which in turn is equal to In what you wrote, you are missing parentheses around the quantity in the denominator, 1 tan 2 (x) What you wrote is the same as #10 symbolipoint

1

Ex 7 2 25 Integrate 1 Cos 2 X 1 Tan X 2 Ex 7 2

 We will use the following trigonometric formula to prove the formula for tan 2x tan (a b) = (tan a tan b)/ (1 tan a tan b) We have tan 2x = tan (x x) = (tan x tan x)/ (1 tan x tan x) = 2 tan x/ (1 tan 2 x) Hence, we have derived the tan 2x formula using the angle sum formula of the tangent functionWe can prove the double angle identities using the sum formulas for sine and Shivam Mishra, Meritnation Expert added an answer, on 26/7/16 Shivam Mishra answered this Dear Student, Please find below the solution to the asked query We have f 2 tanx 1 tan 2 x = cos 2 x 1 sec 2 x 2 tanx 2 = cos 2 x 1 2 1 cos 2 x 2 sinx cosx = cos 2 x 1 2 1 2 sinx cosx cos 2 x = cos 2 x 1 2 1 sin 2 x cos 2 x = 2 cos 2 x 1 1 2 1 sin 2 x cos 2 x = 2 cos 2 x 2 1 sin 2 x cos 2 x f 2 tanx 1 tan 2 x = 1 sin 2 x We know that 2 tanx 1 tanDo NOT divide by sin bc it can equal zero to find a side, you can divide by sin to find theta

Prove Sin2x 2tanx 1 Tan 2x Socratic

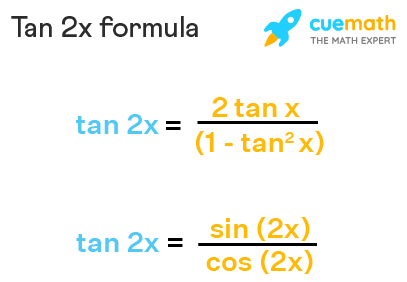
Tan 2x Formula What Is Tan 2x Formula Examples

 Using the tan1 x convention may lead to confusion about the difference between arctangent and cotangent It turns out that arctan and cot are really separate things cot(x) = 1/tan(x) , so cotangent is basically the reciprocal of a tangent, or, in 149 अगर , तो का मूल्य , तो के बराबर है int e^ (x) ( (2 tanx)/ (1tanx)cot^ (2) (x (pi)/ (4)))dx is equal to Updated On 299 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!

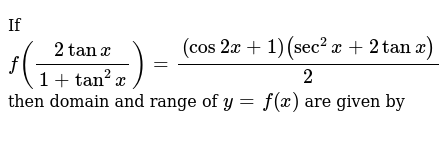
いろいろ Tan2x 1sec2x ただの悪魔の画像

What Is The General Solution Of X For Tan X Tan2x 1 Quora

Sin (b) Cos (a)Cos (b) Therefore, sin (xx) = sin (x)cos (x) cos (x)sin (x) = 2 sin (x) cos (x) Also, Sin 2x = 2 t a n x 1 tan ⁡ 2 x To Prove Sin2x in the form of tanx x which is equal to 2 t a n x 1 tan ⁡ 2 x Now let us start the proof from the righthand side and hence, prove it as LHS = RHSEvaluate $\displaystyle \large \lim_{x \,\to\, \tan^{1}{3}} \normalsize {\dfrac{\tan^2{x}2\tan{x}3}{\tan^2{x}4\tan{x}3}}$Sin^2xcos^2x=1 tan^2x1=sec^2x cot^2x1=csc^2x Some Pythagorean identities can be rewritten when you prove an identity you are trying to figure out how one side of the equations simplify down to equal the other side of the equation, by doing so you are showing all work 2cos^2x1 tan2x= (2tanx) / (1tan^2x)

By Siby Sebastian Pgt Maths Ppt Download

What Is The Formula Of Tan2x Quora

If (2tanx)/(1tan^2 x)=1/sqrt3, then x can be equal to _____ (check all that apply) a) x=5pi/12 npi b) x=7pi/12 npi c) x=11pi/12 npi d) x=pi/12 npi Tan2x=2tanx/1tan^2x Given this circumstance, what is the formula of trigonometry?If x = 30°, verify that (i) tan 2x=(2tan x)/(1tan ^2x) CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3112 Question Bank Solutions 467 Concept Notes & Videos 309 Time Tables 12 Syllabus Advertisement Remove all ads

Prove That Tan 4x 4tanx 1 Tan 2 X 1 6tan 2 X Tan 4 X Sarthaks Econnect Largest Online Education Community

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

 Best answer We have f (2tanx/ (1 tan2x)) = 1/2 (1 cos2x) (sec2x tanx) = 1/2x 2cos2x x (1 tan2x 2tanx) = cos2x x (1 tanx)2 = {cosx x (1 tanx)}2 = (cosx sinx)2 = 1 sin (2x) Thus, f (sin 2x) = 1 sin (2x)10 Here, $ x $ denotes the greatest integer less than or equal to $ x $ Given that $ f(x) = x x $ The value obtained when this function is integrated with respect to $ x $ with lower limit as $ \frac{3}{2} $ and upper limit as $ \frac{9}{2} $ , isTan^2x= 2tanxsinx My work so far tan^2x 2tanxsinx=0 tanx(tanx 2sinx)=0 Then the solutions are TanX=0 and sinX/cosX = 2 sin X Divide through by sinX we have to check this later to see if allowed (ie sinX

bestpictjcry Tan 2x Tan 2x

Fastest What Is Tan 2x Equal To

 Coefficients can be removed when differentiating, ie d/dx 2tanx = 2 d/dx tanx You should know that d/dx tanx = sec2x (either by differentiating sinx/cosx or by just remembering the derivatives of common trig functions, as it will come in handy) Homework Statement cosx=12/13 3pi/2 is less than or equal to x is less than or equal to 2pi Homework Equations sin2x = 2sinxcosx cos2x = 12(sinx)^2 tan2x = (2tanx)/(1(tanx)^2) The Attempt at a Solution Using the tan2x formula, I get 60/47(2tanx / (1 tan 2 x)) = 1 Recall Trigonometry formulas tan2A = (2tanA / (1 tan 2 A)) Substitute (2tanx / (1 tan 2 x

Analytic Trig Ppt Video Online Download

3

 not sure how to start this one, i have tried it a few different ways and i still can't get it (1 tanx)^2 = sec^2x 2tanxAnswer (1 of 3) There is no difference between (tanx)² and tan²x because we can write (tanx)² = tanx tanx Which is equal to tan²x But there are different in tan²x and tanx² Also difference in ( logx )² and logx² We can write (logx)² as = logx logx But in logx² = 2logx If sec(xy),sec(x),sec(xy) are in AP then prove that cosx= √2 cos y/2 where cosx and cosy are not equals to 1, Math How do I solve this?

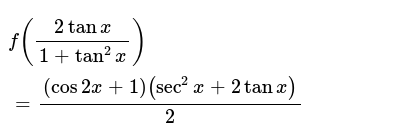
F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2

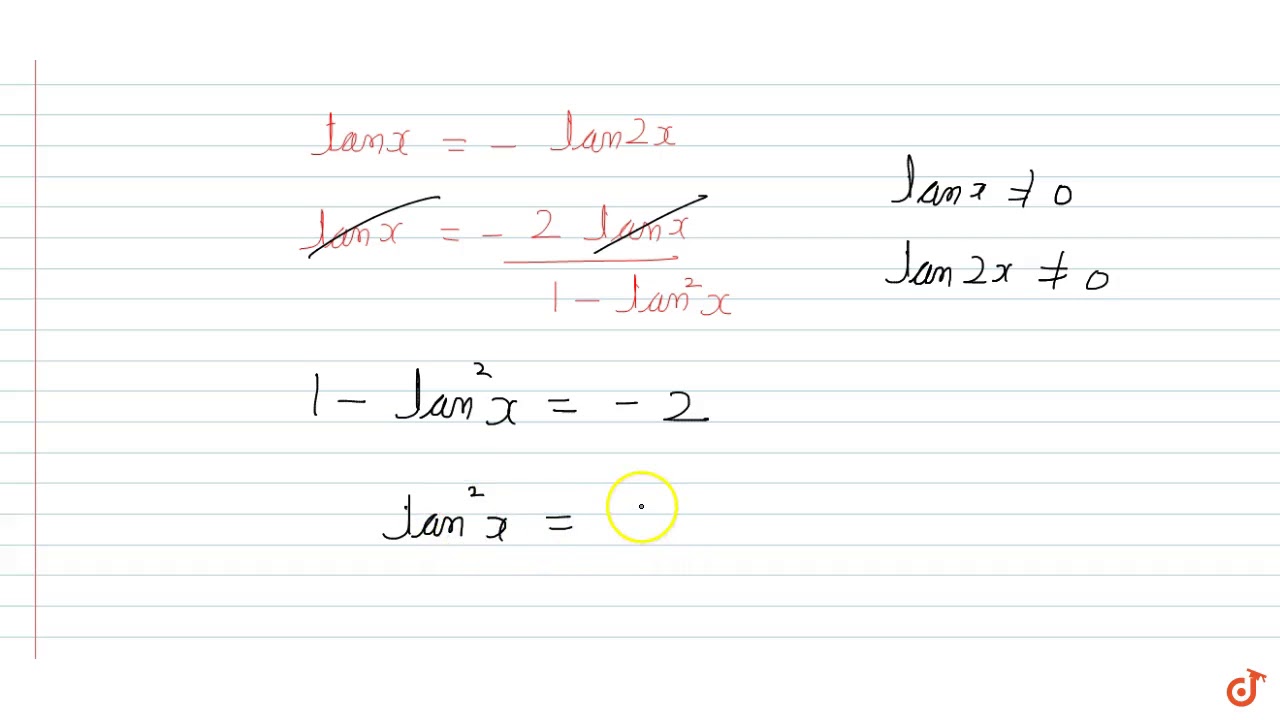
The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is Youtube

 2(sin x / cos x) / 1 – (sin²x / cos²x) = Now tan x = sin x / cos x (2 tan x) / 1 – (sin²x / cos²x) = Remember that tan²x = sin²x / cos²x (2 tan x) / (1 – tan²x) =RHS Hence Proved Alternative method LHS=tan{(2x)} =tan(xx) We know that tan (A B)= tan(A)tan(B) / 1 tan A tan B Applying the same formula we get =>tan(xx)= tan(x)tan(x) / 1 tan x tan x 2tan(x) / (1Basic Trigonometric Function Formulas By using a rightangled triangle as a reference, the trigonometric functions or identities are derived sin θ = Opposite Side/Hypotenuse cos θ = Adjacent Side/Hypotenuse tan θ = Opposite Side/Adjacent SidePlease find below the solution to your problem tan x sec x = √3 squaring on both sides (tan x sec x)^2 = √3^2 tan^2x sec^2x 2tanx sec x = 3 sec^2x tan^2x = 1 tan^2x 1 tan^2x 2tanx secx = 3 2tan^2x 2tanxsecx = 31 tan^2x tanx secx = 2/2

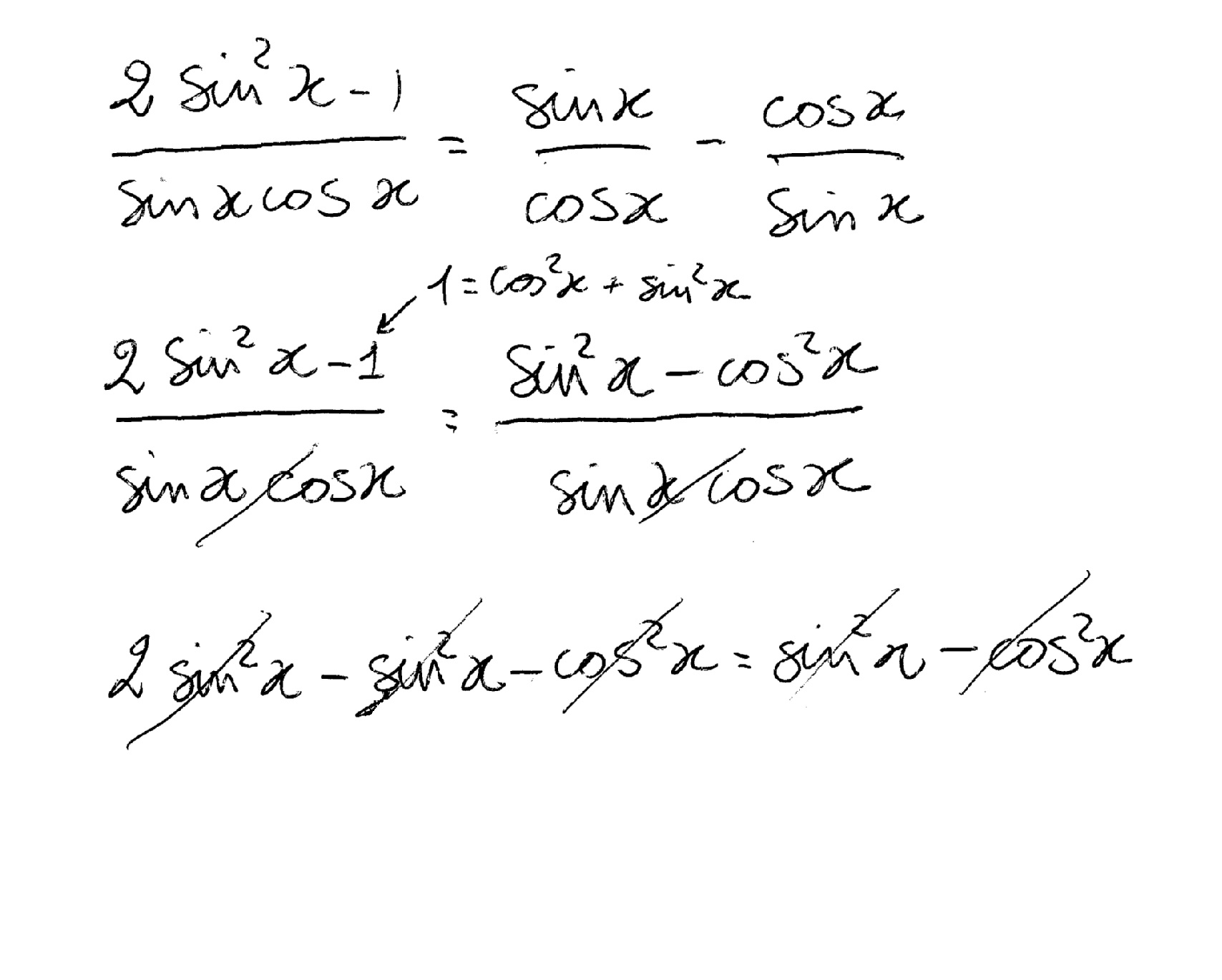
How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

= 2 tan x/(1 tan 2 x) Hence we have derived the tan 2x formula by expressing it as a ratio of sin 2x and cos 2x Graph of Tan 2x The graph of tan 2x looks similar to the graph of tan x We know that the period of tan x is π Since the period of tan bx is given by π/b, the period of tan 2x is π/2 Given below is the graph of tan 2x and Use tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x, for the right hand side expression 2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x) =2 sin x cos x/(cos^2xsin^2x) =(sin 2x)/(cos 2x)=tan 2x Proofs for sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x Use Area of a triangleABC = 1/2(base)(altitude) = 1/2 bc sin A Here, it is the triangle ABC of a unit 5x means 5*xwhat number, when multiplied by 5, will give you 12 To get the value of x, x must stand alone We do so by making x the subjectin other wordswe divide both sides by the coefficient of x which is 5when this is donethe first term's 5 will be ruled out by the 5 dividing the term and then we will be left with an equation like x=

Lim X To 0 2 Tan X 2 Sin X X 2 Sin X Without L Hopital S Rule How Is My Procedure Wrong Mathematics Stack Exchange

Bestpixtajpgjgh If F 2tanx 1 Tan 2x 1 Cos2x Sec 2x 2tanx 2 Then F 4

Take x common and 1cos2x=2(sin^2 x) hence x tan2x 2tanx/{2(sin^2 x)}^2 is the equation) tan2x = 2tanx/(1 tan^2 x) On substituting and simplifying we get x2tanx tan^2 x / (1 tan^2 x)(4 sin^4 x) Write tanx = sinx/cosx On substituting and simplifying we get 2x / 4sinxcosx (cos^2 x sin^2 x) Write cos^2 x = 1 sin^2 x and take Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 taPurplemath In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right trianglesThere are loads of trigonometric identities, but the following are the ones you're most likely to see and use

Fastest What Is Tan 2x Equal To

bestpictjcry Tan 2x Tan 2x

 The integral ∫(sec^2x/(secx tanx)^9/2)dx equals (for some arbitrary constant K) asked in Integrals calculus by Rozy ( 418k points) indefinite integrationTan(AB) = tanAtanB/1tanAtanB From this formula we can derive tan(2x) as tan(xx) So tan(2x)= 2tanx/1tanxtanx We can always go for the longer approch from sinx/cosx toGraph y=1/2*tan (2x) y = 1 2 ⋅ tan (2x) y = 1 2 ⋅ tan ( 2 x) Find the asymptotes Tap for more steps For any y = tan ( x) y = tan ( x), vertical asymptotes occur at x = π 2 n π x = π 2 n π, where n n is an integer Use the basic period for y = tan ( x) y = tan ( x), ( − π 2, π 2) ( π 2, π 2), to find the vertical

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

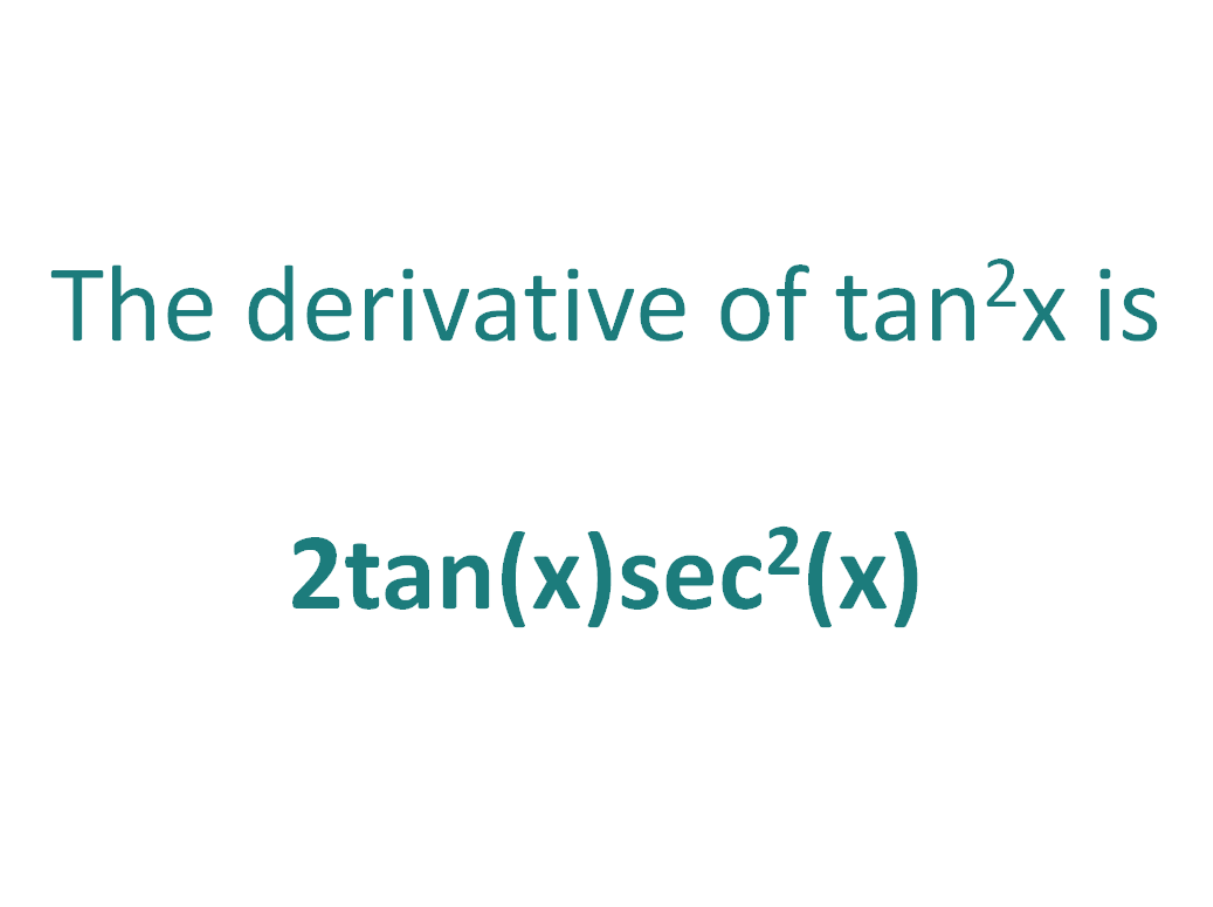
The Derivative Of Tan 2x Derivativeit

Trigonometry Solve for x tan (2x)= (2tan (x))/ (1tan (x)^2) tan(2x) = 2tan(x) 1−tan2 (x) tan ( 2 x) = 2 tan ( x) 1 tan 2 ( x) Since x x is on the right side of the equation, switch the sides so it is on the left side of the equation 2tan(x) 1− tan2(x) = tan(2x) 2 tan ( x) 1 tan 2 ( x) = tan ( 2 x)Squaring both sides, we get, tan 4x−2tan 3xtan 2x=1 ⇒tan 4x−2tan 3x−tan 2x2tanx=12tanx−2tan 2x ∴tan 4x−2tan 3x−tan 2x2tanx1=22(tanx−tan 2x)=12=4 using (1) Hence correct option is 'D' The trigonometric equation is sec 2 (x) tan x = 2tan(x) tan x sec 2 (x) 2 = 0 ⇒tan x = 0 and sec 2 (x) 2 = 0 tan x = 0 tan x = tan 0 The genaral solution of tan(θ) = tan(α) is θ = nπ α, where n is an integer ⇒ x = nπ 0 x = nπn = 0,1,2 sec 2 (x) 2 = 0 sec 2 (x) = 2 Using reciprocal identity sec 2 x = 1/cos

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

1 2tan X 2 1 4 Tanx 4 1 2 X Tan X 2 X

Tan 2x = 2 tan x / (1tan^2x)hence, tan 2x = 12x = pix = pi/2 Two trains leave the station at the same time, one heading west and the other east Explanation 2tanx 1 tan2x = 2 sinx cosx sec2x = 2 sinx cosx 1 cos2x = 2sinx cosx × cos2x 1 = 2sinxcosx = sin2x Answer link

Tan2x 1 ただの悪魔の画像

Chapter 7 Trigonometric Identities And Equations Ppt Download

2tanx Cotx 1 0 Youtube

Pinakamabilis Tan 2x Cot 2x 1

Prove That Sec8x 1 Sec4x 1 Tan8x Tan2x Maths Trigonometric Functions Meritnation Com

Tangent Half Angle Formula Wikipedia

What Is The Formula Of Tan2x Quora

What Is The Formula Of Tan2x Quora

Trig Limit 1 Tanx X Pi 4 Compound Angle Substitution Youtube

いろいろ Tan2x 1sec2x ただの悪魔の画像

View Question Trigonometric Identities

Derivative Of Tan X Old Video Khan Academy

Evaluate X 0 P 2 Tanx 1 M 2tan 2x Dx Sarthaks Econnect Largest Online Education Community

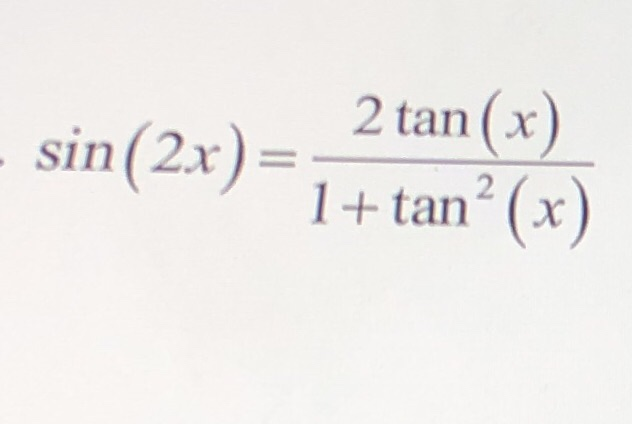
2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

Prove That Tan4x 4tanx 1 Tan 2x 1 6tan X Tan 4x Maths Trigonometric Functions Meritnation Com

How To Take The Derivative Of Tan X Video Lesson Transcript Study Com

How Do You Solve Sec 2x 2tanx 0 Socratic

Tan2x 1 ただの悪魔の画像

1

How To Solve Tan 2x 3tanx 2 0 To Find Tan X Quora

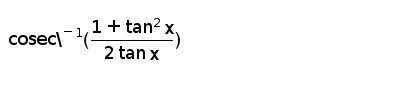
If 2tanx 1 Tan 2x 1 Then X Can Equal

Prove That Tan2x 2tanx 1 Tan 2x Youtube

How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora

Prove That Tan2x 2tanx 1 Tan 2x Youtube

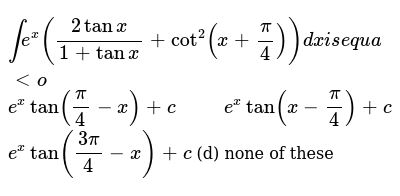
Inte X 2tanx 1 Tanx Cot 2 X Pi 4 Dxi Se Q U A Lto E Xtan Pi 4 X C E Xtan X Pi 4 C E Xtan 3pi 4 X C D None Of These

Solved 25 24 7 Complete The Identity 17 Sin X Cos X 2 Chegg Com

Solve Sinxtanx 1 Tanx Sinx

What Is The Formula Of Tan2x Quora

The Solution Of Differential Equation Dy Dx Y Tanx 2x X 2tanx Is Sarthaks Econnect Largest Online Education Community

If F X Tan 2x Then

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2 Youtube

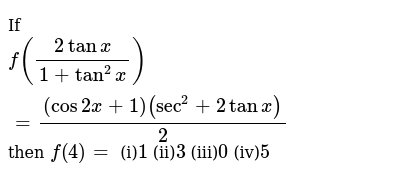
If F 2tanx 1 Tan 2 X Cos2x 1 Sec 2 2tanx 2 Then F 4 I 1 Ii 3 Iii 0 Iv 5

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

Exercise 1 Hy 100 1 X Tw 1 Then Content 17 2 If Y Log Vcosx

Jpsaepictlqtj Tan 2x Formula Tan 2x Formula In Terms Of Cos X

Evaluate Lim X Tan 1 3 Tan X 2tanx 3 Tan X 4tanx 3

Tan2x 1 ただの悪魔の画像

Old Version Trig Show Sin 2x 2 Sin X Cos X 2tan X 1 Tan 2 X Youtube

What Is The General Solution For Tanthanx Tan 2x Tan 3x Quora

Int Sin 1 2tanx 1 Tan 2 X Dx Youtube

The Nearest Degree Tan 2x 2tanx 0 In The Interval 0 X 3pi 2 A 63 180 243 360b 0 63 180 243 360c 63 243d 0 180 360 Study Com

What Is The Formula Of Tan2x Quora

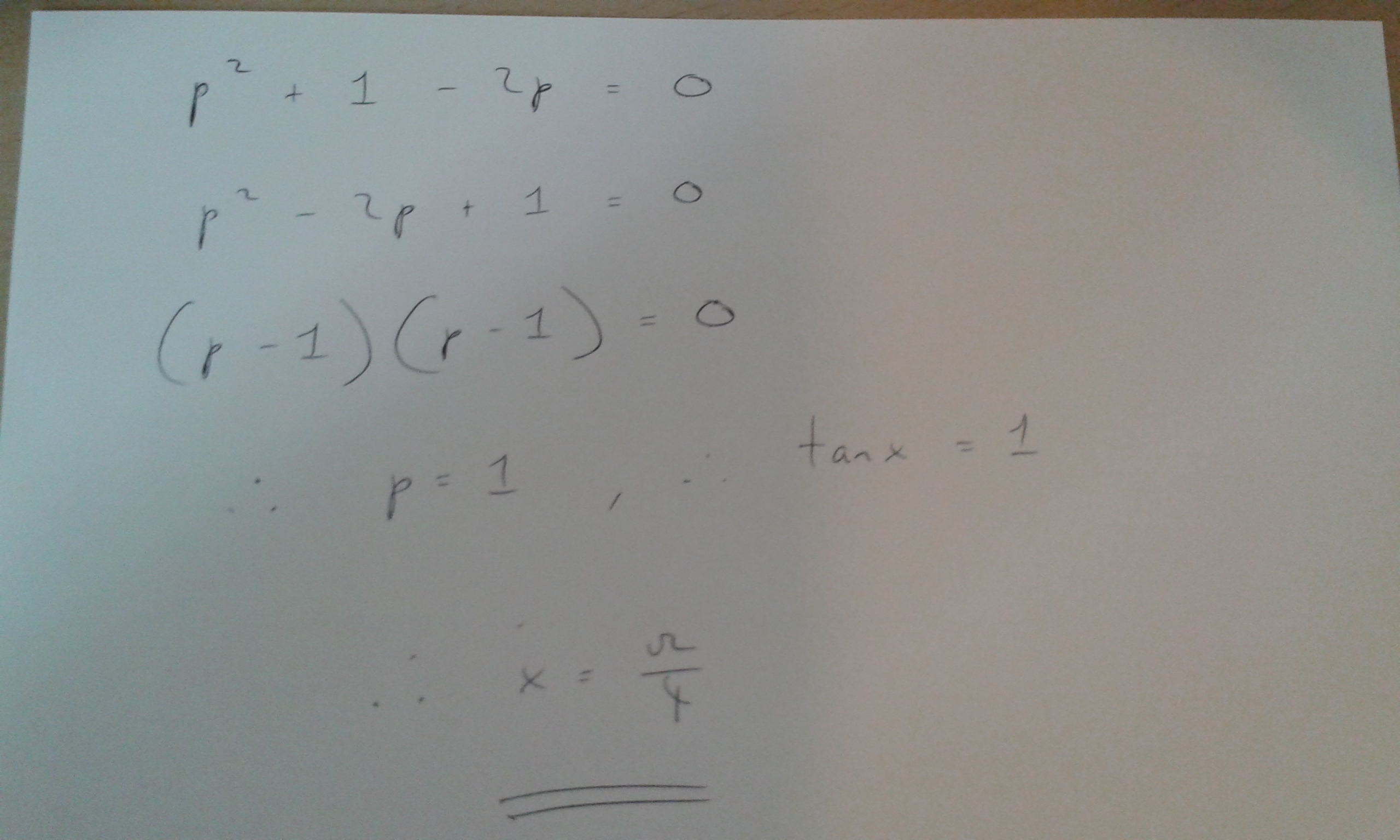
How Do You Solve Sec 2x 2tanx 0 Socratic

1 2tanx Per 1 Tan2x 2 1 Tan2x Per 1 Tan2x Brainly Co Id

Prove That Tan2x 2tanx 1 Tan X Brainly In

Tan2x 1 ただの悪魔の画像

If Tanx 12 13 Evaluate 2 Sinx Cosx Cos 2x Sin 2x

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

Prove That Sin 2x Squared 2tanx Upon 1 Tan Square X Brainly In

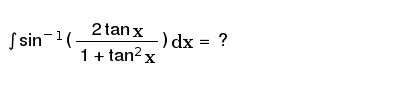
If 2tanx 1 Tan 2x 1 Then X Can Equal

Fastest What Is Tan 2x Equal To

If 2tanx 3tany Then Prove That Tan X Y Homework Help Mycbseguide

Which Of The Following Are Solutions To 2tanx 1 Tan 2x Sqrt 3 Check All That Apply Options Are In Brainly Com

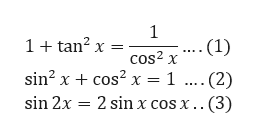
Answered 2x Given Tan X 2 And Cos X Is Less Bartleby

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

If Tan X 2tan 2x 3tan 3x 8cot 8x 3 Then The General Solution Of X

Sin2x Sin 2x Identity For Sin2x In Terms Of Tanx Proof Of Sin2x 2tanx 1 Tan 2x Youtube

1 Tan 2x Sec 2x

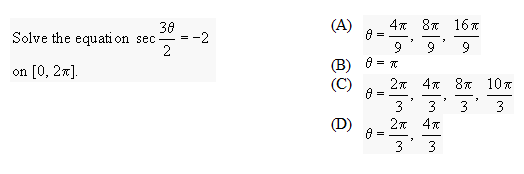
Solved Find All Solutions To The Equation Tan 2x 2tanx 1 0 Chegg Com

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2

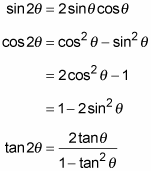
How Do You Prove That Cot2x Tan 2x 1 2tanx Socratic

Solve Cot 2x 0 The Student Room

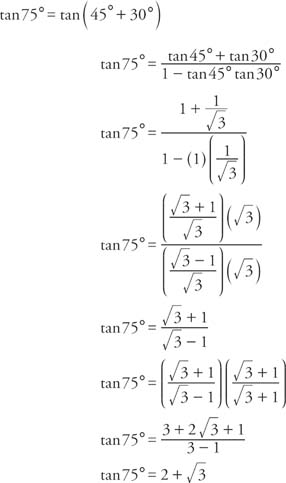
Tangent Identities

Tan2x 1 ただの悪魔の画像

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

How Do You Prove Tan 2x Secx 1 1 Secx Socratic

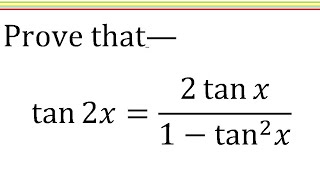
Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

Sec 2 2x 1 Tan2x Youtube

Tan 2x Formula What Is Tan 2x Formula Examples

bestpictjcry Tan 2x Tan 2x